Universal Domain Adaptation
CVPR2019
Abstract
引入一种新的领域自适应方法:通用领域自适应方法UDA,该方法不需要对源和目标域的标签集进行任何先验知识的假设。传统的领域自适应方法通常需要丰富的先验知识,因此在实际应用中受到限制。而通用领域自适应则可以应对更广泛的应用场景。同时作者提出了通用自适应网络UAN,实现共同标签集和私有标签集的分类,将私有标签集的样本标记为未知样本,将共同标签集的样本分类到标签集中。
DA
在现实世界中很难选择合适的DA方法,因为缺少关于目标标签集的先验知识,因此作者提出通用域自适应UDA。
- closed set DA:源标签集和目标标签集相同
- partial DA:目标标签集是源标签集的子集
- open set DA:源标签集是目标标签集的子集
- open-partial DA:源和目标标签集中存在各自私有的标签集和共同的标签集
- universal DA(new):源标签域已知,对于任何目标域,如果属于源标签集中的任何类别,则对其进行正确分类,否则标记为unknown类
同时UDA也面临两个问题:
- 由于不知道目标标签集的内容,因此无法决定源域中的哪个部分和目标域中的哪个部分匹配,而将两个整个的域进行匹配会使得模型效果很差。
- 如果目标标签集不属于任何源标签集,需要标记为unknown,但是对这些未知类没有标记的训练数据,无法区分它们的详细类别。
为此提出通用自适应网络UAN,利用了域相似性和预测不确定性从而配备了一个新的标准来量化每个样本的可转移性。
UDA
一些符号标记
- \(D _ { s } = \left\{ ( x _ { i } ^ { s } , y _ { i } ^ { s } ) \right\}\):源域,包含\(n _ {s}\)个标记的样本,从分布\(p\)中采样
- \(D _ { t } = \left\{ ( x _ { i } ^ { t } ) \right\}\):目标域,包含\(n _ {t}\)个未标记的样本,从分布\(q\)中采样
- \(C _ {s}\):源域的标签集
- \(C _ {t}\):目标域的标签集
- \(C = C _ { s } \cap C _ { t }\)表示两个域共享的标签集,\(\overline { C } _ { s } = C _ { s } /\ C\)表示源域私有的标签集,\(\overline { C } _ { t } = C _ { t } /\ C\)表示目标域私有的标签集
- \(p c _ { s }\)和\(p c\)分别表示\(C _ {s}\)和\(C\)中的标签的源数据分布
- \(q c _ { t }\)和\(q c\)分别表示\(C _ {t}\)和\(C\)中的标签的目标数据分布
-
定义两个域之间的commonness为两个标签集的Jaccard distance:$$ \xi = \frac { C _ { s } \cap C _ { t } } { C _ { s } \cup C _ { t } }\(,\)\xi\(越小,共享的知识越少,适应越困难。UDA的任务是在未知\)\xi\(的情况下,可以在广泛的\)\xi$$值情况下表现良好。
Challenges
- category gap:根源在于标签集的不同,如果用closed set DA解决UDA,源和目标域私有的标签集可能匹配,这明显是不合理的;如果用partial DA或open set DA解决,缺乏源域和目标域的对应关系也就是先验知识,所以也不可行;因此需要自动识别源数据和目标数据,以便在公共标签域上进行对齐。
- domain gap:源数据的分布和目标数据的分布不同。
- “unknown” classes:常用的通过标记分类置信度较低的样本为unknown的方法可能不适用于UDA,因为神经网络的预测通常会overconfident,判别性较差。
UAN
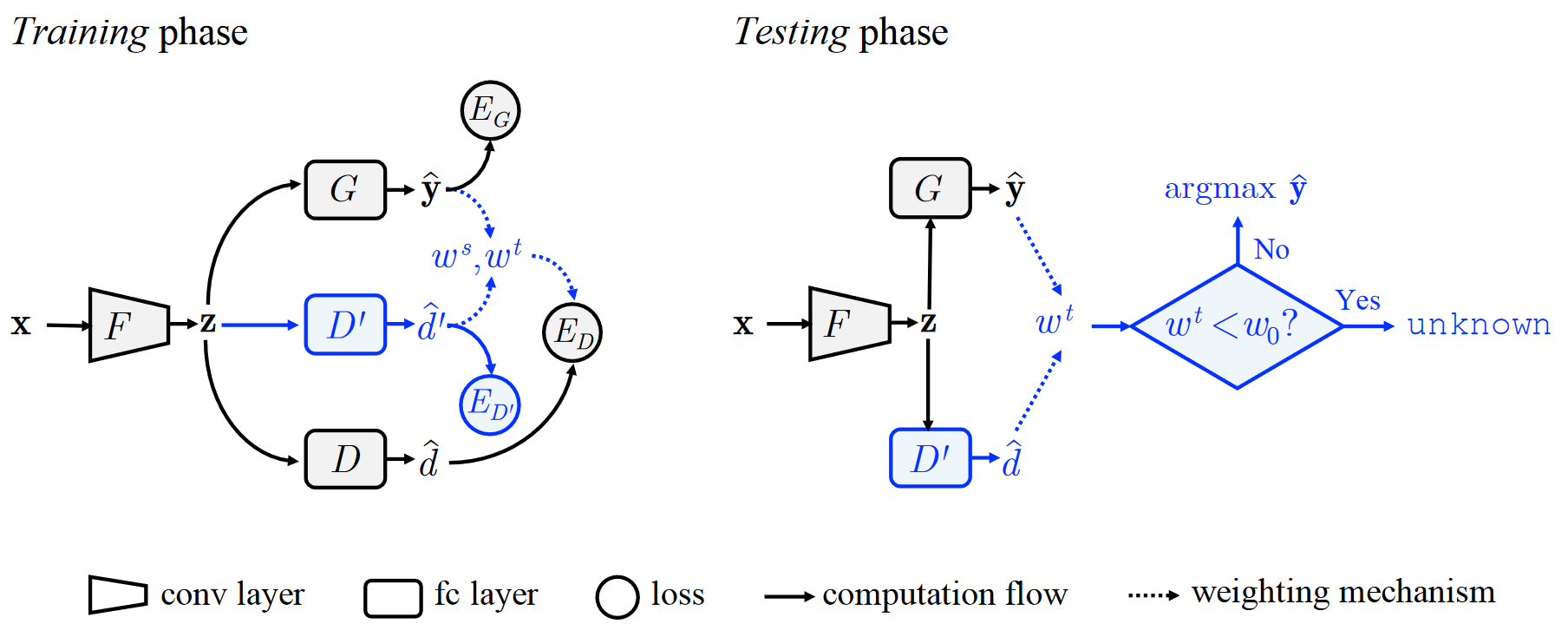
由特征提取器\(F\)、对抗域判别器\(D\)、非对抗域判别器\(D ^ { \prime }\)和一个标签分类器\(G\)组成。
\(F\):努力使\(D\)混淆,在公共标签集\(C\)中产生不变性特征,在这种特征上训练的标签分类器\(G\)可以安全应用于目标域。
\(D\):在公共标签集\(C\)中区分源数据和目标数据
\(D ^ { \prime }\):预测源样本域为1,目标样本域为0,因此\(\widehat { d ^ { \prime }}\)可以被视为域相似度,\(\widehat { d ^ { \prime }}\)越小意味着与目标域越相似,越大意味着与源域越相似
train
来自任意域的输入\(x\)会输入到特征提取器\(F\)中,提取到的特征\(z = F ( x )\)会被馈入到标签分类器\(G\)中,获得输入\(x\)关于源类\(C _ {s}\)的概率\(\widehat { y } = G ( z )\);非对抗域判别器\(D ^ { \prime }\)获取域相似度\(\widehat { d ^ { \prime } }= D ^ { \prime } ( z )\),量化了输入\(x\)与源域的相似性;对抗域判别器\(D\)在共同标签集\(C\)中匹配源数据和目标数据的特征分布(需要一个机制来检测共同标签集),\(E _ { G }\), \(E _ { D ^ { \prime } }\)和\(E _ { D }\)表示三个过程的error,定义如下: \(E _ { G } = E _ { ( x , y ) \sim p } L ( y , G ( F ( x ) ) )\)
\[E _ { D ^ { \prime } } = - E _ { x \sim p } \log D ^ { \prime } ( F ( x ) ) - E _ { x \sim q } \log ( 1 - D ^ { \prime } ( F ( x ) ) )\] \[E _ { D } = - E _ { x \sim p } w ^ { s } ( x ) \log D ( F ( x ) ) - E _ { x \sim q } w ^ { t } ( x ) \log ( 1 - D ( F ( x ) ) )\]其中\(L\)是标准交叉熵损失,\(w ^ { s } ( x )\)和\(w ^ { t } ( x )\)分别表示源样本和目标样本属于公共标签集\(C\)的概率。
模型目标
\[\begin{matrix} \max _ { D } \min _ { F , G } E _ { G } - \lambda E _ { D } \end{matrix} \\ \min _ { D ^ { \prime } } E _ { D ^ { \prime } }\]\(\lambda\)是在迁移性和判别性之间进行权衡的超参数。
test
给定每个目标样本\(x\)输入到特征提取器\(F\)中,提取到的特征\(z = F ( x )\)会被馈入到标签分类器\(G\)中,获得输入\(x\)关于源类\(C _ {s}\)的概率\(\widehat { y } = G ( z )\);非对抗域判别器\(D ^ { \prime }\)获取域相似度\(\widehat { d } ^ { \prime } = D ^ { \prime } ( z )\),计算出\(w ^ { t } ( x )\)通过与验证阈值\(w _ {0}\)比较得到预测的类,小于阈值标记为unknown,大于阈值分类到源类中。
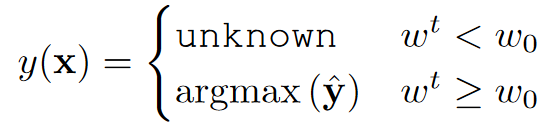
transferability criterion
通过一个适当的样本级可转移性标准计算权重\(w ^ { s } ( x )\)和\(w ^ { t } ( x )\),源域和目标域中的每个点都可以加权,使得共享标签集中源数据和目标数据的分布可以最大程度对齐;同时来自目标私有标签集的数据也可以被识别并标记为unknown。该标准满足下述方程: \(E _ { x \sim p _ {C} } w ^ { s } ( x ) > E _ { x \sim p _ {\overline { C _ {s}}} } w ^ { s } ( x )\)
\[E _ { x \sim q _ { C } } w ^ { t } ( x ) > E _ { x \sim q _ {\overline { C _ {t}}} } w ^ { t } ( x )\]Domain Similarity:假设\(E _ { x \sim p _ {\overline { C _ {s}}} }\widehat { d ^ { \prime }} > E _ { x \sim p _ {C} }\widehat { d ^ { \prime }} > E _ { x \sim q _ {C} }\widehat { d ^ { \prime }} > E _ { x \sim q _ {\overline { C _ {t}}} }\widehat { d ^ { \prime }}\)
Prediction Uncertainty:熵量化了预测的不确定性,熵越小意味着更自信的预测,假设\(E _ { x \sim q _ {\overline { C _ {t}}} } H ( \widehat { y } ) > E _ { x \sim q c } H ( \widehat { y } ) > E _ { x \sim p c } H ( \widehat { y } ) > E _ { x \sim p _ {\overline { C _ {s}}} } H ( \widehat { y } )\)
综上:熵被归一化并与域相似度度量进行比较。 \(w ^ { s } ( x ) = \frac { H ( \widehat { y } ) } { \log | C _ { s } | } - \widehat { d } ^ { \prime } ( x )\)
\[w ^ { t } ( x ) = \widehat { d ^ { \prime }} ( x ) - \frac { H ( \widehat { y } ) } { \log | C _ { s } | }\]Implementation Details
backbone:ResNet-50
