反卷积（deconv）

也叫转置卷积，用于还原出卷积之前的图片尺寸，可用于upsample等任务。

卷积的shape计算公式：\(o = \frac { i - k + 2 \ast p } { s } + 1\)

反卷积的shape计算公式：\(i = ( o - 1 ) \ast s + k - 2 \ast p\)

因果卷积（causal conv）

在传统CNN中的全连接违背了时间先后顺序的约束，也就是前一时刻的输出与后一时刻的输出相互产生了连接。可以通过mask的方式，只保留从前往后的链接，这就满足了时间上的前后依赖。

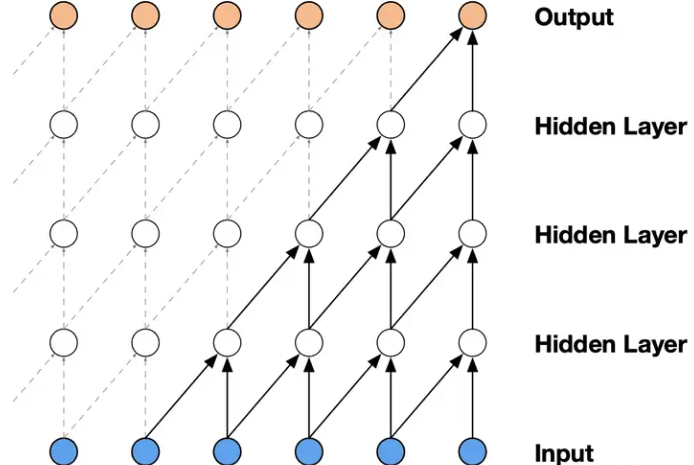
存在的问题：因果卷积对历史信息的覆盖范围不大，会浪费更前面的输入信息。通过不断增加网络层数可以解决这个问题，但是同样的使得网络的训练参数变多，网络规模越来越大。

时序卷积（Temporal conv）

import torch.nn as nn
from torch.nn.utils import weight_norm


# 裁剪模块，裁剪掉多余的padding
class Chomp1d(nn.Module):
    def __init__(self, chomp_size):
        super(Chomp1d, self).__init__()
        self.chomp_size = chomp_size

    def forward(self, x):
        return x[:, :, :-self.chomp_size].contiguous()


# 相当于一个残差网络模块
class TemporalBlock(nn.Module):
    def __init__(self, n_inputs, n_outputs, kernel_size, stride, dilation, padding, dropout=0.2):
        super(TemporalBlock, self).__init__()
        self.conv1 = weight_norm(nn.Conv1d(n_inputs, n_outputs, kernel_size,
                                           stride=stride, padding=padding, dilation=dilation))
        self.chomp1 = Chomp1d(padding)
        self.relu1 = nn.ReLU()
        self.dropout1 = nn.Dropout(dropout)

        self.conv2 = weight_norm(nn.Conv1d(n_outputs, n_outputs, kernel_size,
                                           stride=stride, padding=padding, dilation=dilation))
        self.chomp2 = Chomp1d(padding)
        self.relu2 = nn.ReLU()
        self.dropout2 = nn.Dropout(dropout)

        self.net = nn.Sequential(self.conv1, self.chomp1, self.relu1, self.dropout1,
                                 self.conv2, self.chomp2, self.relu2, self.dropout2)
        self.downsample = nn.Conv1d(n_inputs, n_outputs, 1) if n_inputs != n_outputs else None
        self.relu = nn.ReLU()
        self.init_weights()

    def init_weights(self):
        self.conv1.weight.data.normal_(0, 0.01)
        self.conv2.weight.data.normal_(0, 0.01)
        if self.downsample is not None:
            self.downsample.weight.data.normal_(0, 0.01)

    def forward(self, x):
        out = self.net(x)
        res = x if self.downsample is None else self.downsample(x)
        return self.relu(out + res)


# TCN网络模块
class TemporalConvNet(nn.Module):
    def __init__(self, num_inputs, num_channels, kernel_size=2, dropout=0.2):
        super(TemporalConvNet, self).__init__()
        layers = []
        num_levels = len(num_channels)
        for i in range(num_levels):
            dilation_size = 2 ** i
            in_channels = num_inputs if i == 0 else num_channels[i-1]
            out_channels = num_channels[i]
            layers += [TemporalBlock(in_channels, out_channels, kernel_size, stride=1, dilation=dilation_size,
                                     padding=(kernel_size-1) * dilation_size, dropout=dropout)]

        self.network = nn.Sequential(*layers)

    def forward(self, x):
        return self.network(x)

扩展卷积（dilated conv）

扩展卷积可以有效解决上述因果卷积的问题，其主要作用是在不增加参数和模型复杂度的条件下，可以指数倍的扩大视觉野。原理是通过在卷积核移动的过程中加入步长间隔dilation，

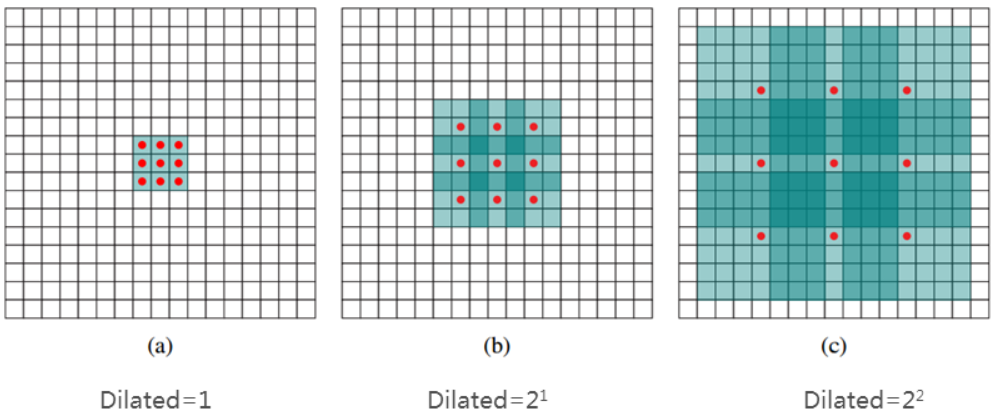
上图中(a)对应3x3的1-dilated conv，也就是传统的conv操作；(b)对应3x3的2-dilated conv，实际的kernel还是3x3，但是dilation为1，也就是对于一个7x7的图像patch，只有9个红色的点与kernel进行卷积操作，略过其他的点；(c)的dilation为4，达到15x15的感受野。

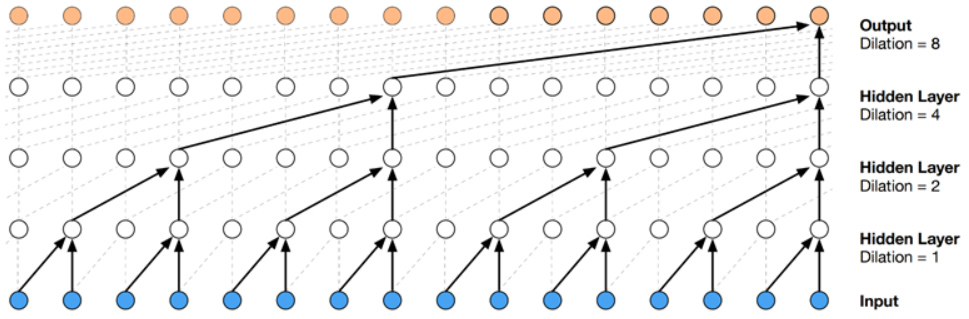
上图是WaveNet中的dilated conv

图卷积（graph conv）

图卷积是处理非结构化数据的大利器。图中的每个结点无时无刻不因为邻居和更远的点的影响而在改变着自己的状态直到最终的平衡，关系越亲近的邻居影响越大。

拉普拉斯矩阵(L)：图的度矩阵(D)减去邻接矩阵(A)。

\[H ^ { l + 1 } = \sigma ( D ^ { - \frac { 1 } { 2 } } \widehat { A } D ^ { - \frac { 1 } { 2 } } H ^ { l } W ^ { l } )\]

对于这里的拉普拉斯矩阵(Symmetric normalized Laplacian) \(L ^ { s y m } = D ^ { - \frac { 1 } { 2 } } \widehat { A } D ^ { - \frac { 1 } { 2 } } = D ^ { - \frac { 1 } { 2 } } (D - A)D ^ { - \frac { 1 } { 2 } } = I _{n} - D ^ { - \frac { 1 } { 2 } }AD ^ { - \frac { 1 } { 2 } }\) 上式引入自身度矩阵，解决自传递问题；同时对邻接矩阵进行归一化，通过对邻接矩阵两边乘以节点的度开方取逆得到。